Numerics for the two-phase Stefan problem

Introduction

The following videos show the evolution of enthalpy h in the two-phase Stefan problem with no-flux boundary in 2D: \begin{cases} h_t(x,t) - \Delta \chi(h(x,t)) = f(x,t), & \text{in } \Omega \times (0, T)\\ \frac{\partial \chi(u)}{\nu} = 0, & \text{on } \partial \Omega \times (0,T)\\ h(x,0) = h_0(x), \end{cases} where h is the enthalpy, f is the volumetric heat source and \chi(h) is the temperature. The function \chi is defined as \chi(s) = \min(s, \max(0, s -1)) = \begin{cases} s & s < 0,\\ 0 & 0 \leq s \leq 1 & s-1 & s > 1, \end{cases} see figure 1.

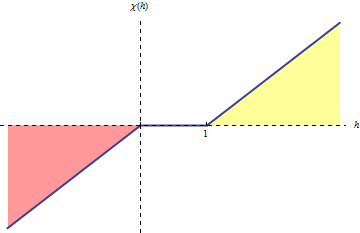
The solutions contain the following regions:

• solid – red
• liquid – yellow
• mushy region – blue

Images were produced using Mathematica 7 and encoded using mencoder. To view these videos, you need to be able to play videos from youtube.

Videos