応用数理プログラム
 応用数理プログラムの紹介
応用数理プログラムの紹介
応用数理とは
〜 数学×プログラミング 〜
応用数理プログラムでは、数学とコンピュータを用いて数理的課題にアプローチする強力な研究者グループを形成し、数学×プログラミングをキーワードに、組合せ論・トポロジー・整数論、数値解析・数理モデリング、現象数理・偏微分方程式の研究を行っています。

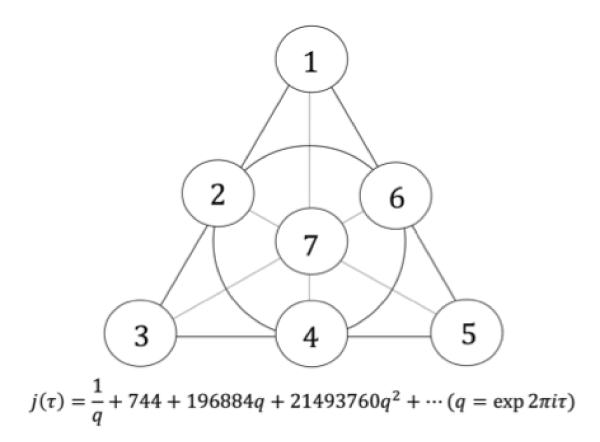
組合せ論・トポロジー・整数論
この分野は、現在の計算科学や情報科学を支えている重要な研究分野で、互いに深く結びついています。例えば整数論で重要な楕円j-関数は、楕円曲線という図形から構成される関数で、無限級数に展開するとその係数が「モンスター群」という組合せ論的対象と結び付いています。楕円j-関数の周辺では数学界のノーベル賞と呼ばれるフィールズ賞受賞者が多く輩出されています。研究室では少人数のセミナーを中心として教育・研究が進められます。具体的には研究室メンバーが専門的な文献の内容を発表し合い理解を深めていく輪講が行われます。同時に、新しい数理現象の発見を目指し、コンピュータを活用した計算も進めています。
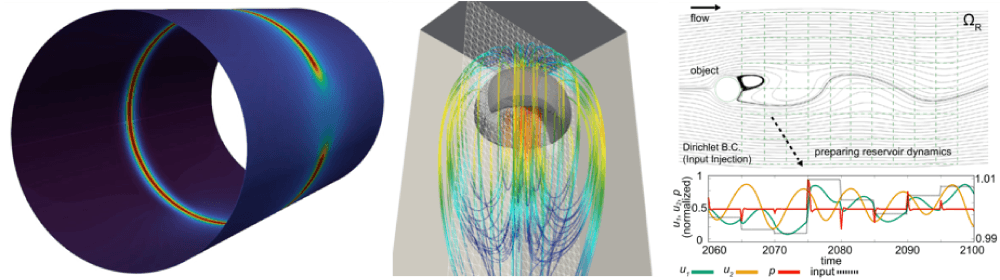
数値解析・数理モデリング&現象数理・
偏微分方程式
この分野は、数学の持つ抽象性を活用して、社会現象・自然現象・生命現象などがもつ特徴量や数理的な構造を顕在化することにより、数理科学分野における新しい理論の創出・構築を目指しています。そこには、抽象理論だけでなく、高度な近似理論を背景とした数値シミュレーション手法の開発・解析・実装の研究も含まれています。数学理論とプログラミングを両輪として、現れる非線形現象を数学的に定式化し、数学理論や近似理論を展開したのち、数値シミュレーションによって具現化する研究を行っています。このような研究アプローチは社会的な要請が強いデータサイエンス分野においても極めて有効で、データサイエンスと親和性の高い数学理論の創出・構築の研究も行われています。